探索对数函数的定义域及求解方法（定义域的重要性和求解方法的应用）

摘要： 对数函数是高中数学中重要的函数之一，它在许多实际问题中有着广泛的应用。而对于对数函数的定义域，它决定了函数的可行取值范围，是我们研究和应用这个函数时必须要了解和掌握的重要内容。本文...

对数函数是高中数学中重要的函数之一，它在许多实际问题中有着广泛的应用。而对于对数函数的定义域，它决定了函数的可行取值范围，是我们研究和应用这个函数时必须要了解和掌握的重要内容。本文将探索对数函数的定义域以及求解方法，并讨论其在实际问题中的应用。

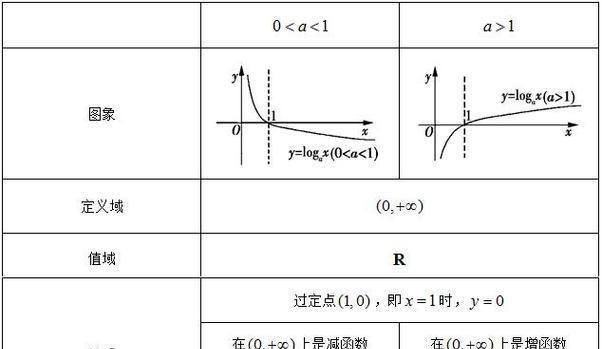
了解对数函数

对数函数是以某个正数为底的指数函数的逆运算，用来描述指数运算中未知指数的求解过程。它常用于解决指数方程、计算复利等问题，具有广泛的应用领域。

对数函数的定义域概念

对数函数的定义域是指在给定的条件下，使函数表达式有意义的实数取值范围。对于常见的对数函数，如以10为底的常用对数函数log、以自然常数e为底的自然对数函数ln等，它们的定义域一般是正实数。

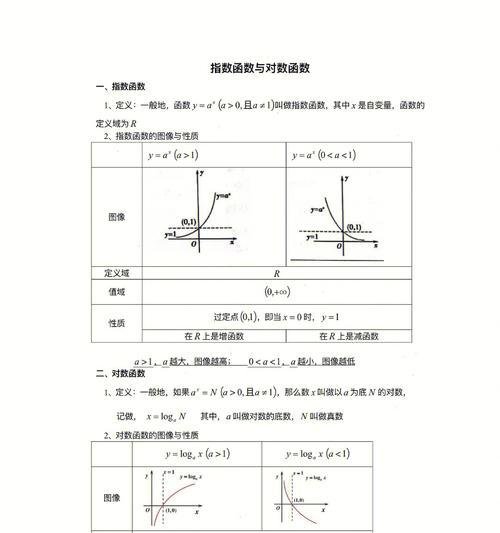
常用对数函数的定义域求解方法

对于以10为底的对数函数log，它的定义域为正实数，即x>0；对于以自然常数e为底的自然对数函数ln，它的定义域也是正实数。我们可以通过观察底数和函数性质来推导出对数函数的定义域。

对数函数的性质与定义域

对数函数具有一些重要的性质，如单调性、奇偶性、零点等。这些性质与定义域密切相关，通过研究函数图像和性质，我们可以更加深入地理解和确定对数函数的定义域。

对数函数在指数方程中的应用

对数函数在解决指数方程中起到了重要的作用。通过将指数方程转化为对数方程，可以简化问题的求解过程，并得到精确的解。对数函数的定义域在指数方程求解中具有重要的意义。

对数函数在复利计算中的应用

复利是金融和投资领域中常见的概念，而对数函数在复利计算中有着广泛的应用。通过应用对数函数的定义域，可以计算出不同时间间隔下的复利利率，进而帮助人们做出更加准确的投资决策。

对数函数在科学计算中的应用

对数函数广泛应用于科学计算中，例如在物理、化学等领域的实验数据处理和模型建立中，对数函数的定义域帮助我们确定变量的合理取值范围，从而得到更加准确和可靠的研究结果。

对数函数在信息论中的应用

对数函数在信息论中有着重要的地位，它被用来衡量信息的量和难以置信度。定义域的确定在信息论中非常关键，它决定了信息传递过程中的可行操作和可靠性。

对数函数的定义域求解方法

通过观察对数函数的底数、性质和应用场景，我们可以推导出对数函数的定义域。起来，一般来说，对数函数的定义域为正实数。

对数函数的定义域问题讨论

尽管对数函数的定义域一般为正实数，但在特殊情况下，如负底数对数、复数底数对数等，定义域可能存在一定的限制和扩展。这些情况需要根据具体问题进行讨论和分析。

对数函数定义域的拓展问题

对数函数的定义域拓展问题涉及到更加复杂的数学领域，如复数、无穷大等概念的引入。这些问题需要在深入研究数学理论的基础上进行探索和解决。

定义域与函数的连续性关系

定义域是决定函数连续性的重要因素之一。对于对数函数来说，其定义域的确定直接影响了函数是否连续。我们可以通过分析定义域来研究对数函数的连续性。

定义域与函数的可导性关系

定义域也与函数的可导性密切相关。对数函数在其定义域内一般是可导的，因为其导数具有良好的性质。我们可以通过定义域来判断对数函数是否可导。

对数函数定义域求解方法的应用

通过求解对数函数的定义域，我们可以更好地理解和应用对数函数。它在解决实际问题、优化计算过程等方面都有着重要的作用。

结语

对数函数的定义域是我们研究和应用该函数时必须要了解和掌握的重要内容。通过对定义域求解方法的研究和应用，我们可以更好地理解和应用对数函数，为解决实际问题提供有力支持。