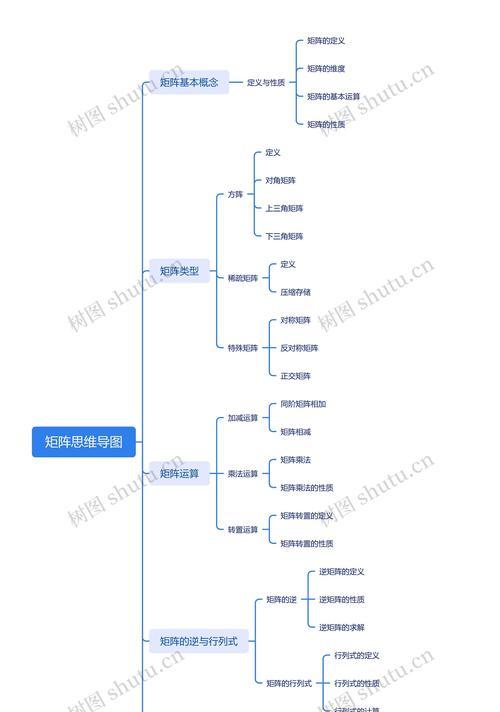
探索常见矩阵类型及其应用领域（了解矩阵的定义和基本特性，探索其在各个学科中的应用）

摘要： 矩阵是数学中的一种基本概念，它在各个领域中都有着广泛的应用。本文将介绍常见的矩阵类型，包括方阵、对称矩阵、零矩阵等，并探索它们在数学、物理、计算机科学等学科中的具体应用。一...

矩阵是数学中的一种基本概念，它在各个领域中都有着广泛的应用。本文将介绍常见的矩阵类型，包括方阵、对称矩阵、零矩阵等，并探索它们在数学、物理、计算机科学等学科中的具体应用。

一、方阵（关键字：方阵）

方阵是最常见的矩阵类型，它具有相同的行数和列数。本节将介绍方阵的定义、性质和特殊形式，包括单位矩阵、对角矩阵等，并探讨它们在线性代数中的应用。

二、对称矩阵（关键字：对称矩阵）

对称矩阵是一种特殊的方阵，它的转置等于它本身。本节将介绍对称矩阵的定义和性质，并探讨它在几何学、物理学和机器学习中的应用。

三、零矩阵（关键字：零矩阵）

零矩阵是一种特殊的矩阵，它的所有元素都为零。本节将介绍零矩阵的性质和特点，并探讨它在矩阵运算和线性方程组中的应用。

四、单位矩阵（关键字：单位矩阵）

单位矩阵是一种特殊的对角矩阵，其主对角线上的元素都为1，其它元素都为0。本节将介绍单位矩阵的定义和性质，并探讨它在线性代数和图论中的应用。

五、稀疏矩阵（关键字：稀疏矩阵）

稀疏矩阵是一种元素大部分为零的矩阵，只有少数非零元素。本节将介绍稀疏矩阵的定义和表示方法，并探讨它在计算机科学和网络分析中的应用。

六、特殊矩阵（关键字：特殊矩阵）

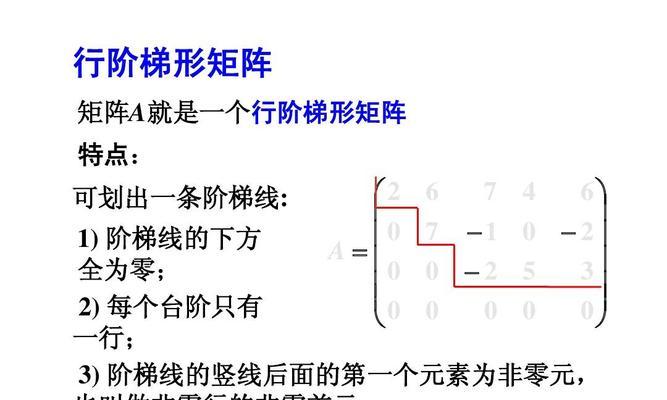
特殊矩阵是指具有一些特殊性质或结构的矩阵类型，如三角矩阵、正交矩阵等。本节将介绍特殊矩阵的定义和特点，并探讨它们在线性代数、信号处理等领域中的应用。

七、厄米特矩阵（关键字：厄米特矩阵）

厄米特矩阵是一种特殊的对称矩阵，其转置和共轭相等。本节将介绍厄米特矩阵的定义和性质，并探讨它在量子力学和通信系统中的应用。

八、正定矩阵（关键字：正定矩阵）

正定矩阵是一种特殊的对称矩阵，其所有特征值都大于零。本节将介绍正定矩阵的定义和性质，并探讨它在优化算法和统计学中的应用。

九、奇异值分解（关键字：奇异值分解）

奇异值分解是一种重要的矩阵分解方法，可以将一个任意形状的矩阵分解为三个矩阵的乘积。本节将介绍奇异值分解的定义和计算方法，并探讨它在数据压缩和图像处理中的应用。

十、矩阵乘法（关键字：矩阵乘法）

矩阵乘法是矩阵运算中的基本操作，其定义和性质对于理解矩阵的运算规则非常重要。本节将介绍矩阵乘法的定义和性质，并探讨它在线性代数和图论中的应用。

十一、特征值与特征向量（关键字：特征值与特征向量）

特征值与特征向量是矩阵理论中的重要概念，它们与矩阵的性质和变换密切相关。本节将介绍特征值与特征向量的定义和性质，并探讨它们在物理学和图像处理中的应用。

十二、矩阵求逆（关键字：矩阵求逆）

矩阵求逆是求解线性方程组和计算矩阵的逆矩阵的关键操作。本节将介绍矩阵求逆的定义和计算方法，并探讨它在解析几何和线性回归中的应用。

十三、矩阵的迹（关键字：矩阵的迹）

矩阵的迹是矩阵主对角线上元素的和，它具有一些重要的性质和应用。本节将介绍矩阵的迹的定义和性质，并探讨它在统计学和量子力学中的应用。

十四、矩阵分解（关键字：矩阵分解）

矩阵分解是将一个矩阵分解为若干个特殊形式的矩阵的乘积，它在数据分析和机器学习中起着关键作用。本节将介绍矩阵分解的定义和常见方法，并探讨它们在推荐系统和图像处理中的应用。

十五、

通过对常见矩阵类型的介绍和应用领域的探索，我们可以看到矩阵作为一种基本的数学工具，在各个学科中都有着广泛的应用。深入了解和掌握不同类型的矩阵及其特性，对于学术研究和实际问题的解决都具有重要意义。